Non-Local Light-Matter interactions
In quantum optics, great effort is being invested toward enhancing the interaction of quantum emitters with light. Different approaches include increasing the number of emitters, the laser intensity, or the local photonic density of states at the location of an atom-like localized emitter. However, the quantum nature of electrons both in free space, and in crystals, force extended wavefunctions for the electrons. These extended electrons, which are defined by their momentum, or pseudo-momentum can emit or absorb light through a process which is momentum conserving, and non-local in space.
The non-local light matter interactions of free electrons relate to several different phenomena: the Cherenkov process, inverse Cherenkov process, and the smith Purcell effect. In our lab we have investigated these processes from several different perspectives. In the base of all these phenomena rely the conversations of momentum of the nonlocal process. Publications include:
Observation of the Stimulated Quantum Cherenkov Effect, Accelerated-Cherenkov radiation and signatures of radiation reaction, Nonperturbative Quantum Electrodynamics in the Cherenkov Effect, and Controlling Cherenkov angles with resonance transition radiation.
Apart of these advancements, there is a large interest to investigate non-local light matter interactions of light with bound electrons. However, optical transitions facilitated by free space photons are nearly direct, owing to their small momentum: as a consequence, the associated energy change of the transitioning electron is fixed by the photon frequency—while its momentum change is negligible. As a result, the transition dynamics of the electron can be accurately captured by a local dielectric function that depends only on the transition frequency ω and is independent of the photon momentum. In contrast to this, several studies have revealed the breakdown of the local paradigm, in deeply nanoscopic plasmonic structures, whose behavior necessitates an account of the material nonlocal response (generally described by the spatial dispersion of ε(r,r’,ω) that includes two space coordinates r,r’). In translationally invariant systems, where ε(r,r’,ω)=ε(r-r’,ω) , nonlocal response is equivalent to an explicit non-local dielectric function.
In our lab, we investigate theoretically whether it is possible to “induce” a nonlocal response or control the intrinsic nonlocality of a material by coupling it to an adjacent polaritonic material. The first work in this subject discussed the Control of semiconductor emitter frequency by increasing polariton momenta. In this paper, we showed that graphene placed near a quantum-well induces a pronounced shift in the emission\absorption frequency. The high momenta of graphene plasmons reaches the electron’s momenta, enabling indirect optical transitions and inducing structural nonlocal properties.
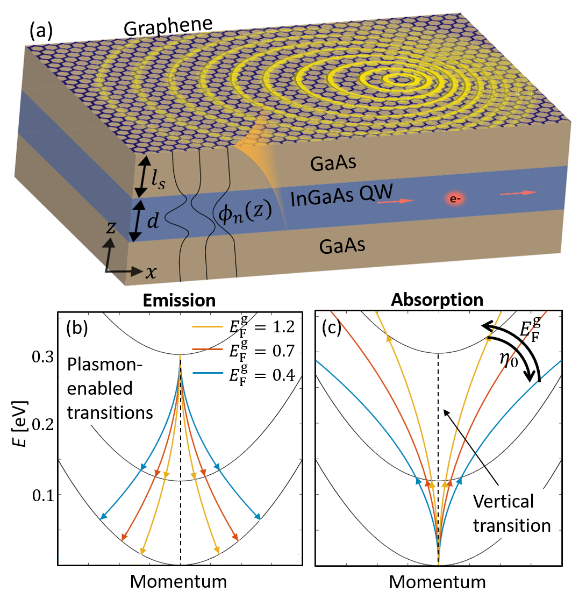
Non-local coupling of graphene plasmon polaritons to a quantum well (QW). a. Scheme of the structure—a graphene layer situated above a GaAs/InGaAs/ QW. Plasmons supported by the graphene layer are illustrated by yellow waves. The z profiles of the QW eigenmodes .b,c. Plasmon emission (b) and absorption (c) between the QW subbands (black) for different graphene Fermi levels (blue =0.4, red 0.7, yellow 1.2 eV).
From a fundamental point of view, the momentum conserving emission include an even broader importance of the work: a first suggestion for non-local light-matter interactions in solids and a first exploitation of electron’s non-locality in solids for light emission. Until this work, the emission from semiconductors was treated as a 2-level system, similar to an atom. The conventional approach to enhance the emission process was to maximize the electric field in the location of an atomic emitter according to the Purcell effect. However, in in non-local interactions, the interaction is enhanced due to a momentum conservation process between the electrons in the solid and the polariton, going beyond the dipole approximation. Such momentum-conserving interaction is completely non-local in space; it occurs through an overlap between the electron wavefunction and the polariton wave, an essentially phase-matching condition in the emission process. Consequently, the emission rate is enhanced not only by reducing the light’s size, but rather by enabling many final states for each initial electron, as appose to the common 2-level approach.
Next, we wanted to investigate what can be the maximal polariton emission in these nanostructures, a path that eventually lead to a publication in Nature Physics. For enhancing the interaction, I improved the matter part by looking at the interband transition (conduction to heavy-hole). In addition, we maximized the polaritonic density of states by adding a perfect conductor on the bottom of the quantum well to confine the optical mode between the graphene sheet and the perfect conductor (sometimes called acoustic plasmons). In order to analyze such intense interaction, we had to expand the theory of the previous work into a full-time dynamical model that include all perturbation theory orders. Eventually, we found that the extreme interaction strength was even stronger than expected: it enables a single conduction electron to interact with all possible un-occupied states and all momentum-conserving related optical modes, unveiling a new coupling regime named non-local ultra-strong coupling (shown in Figs a-d below).
The basic concept that allows such a unique interaction is that energy exchange from the electron to the plasmon can occur before conservation of energy kicks in if the interaction is strong enough. Therefore, by increasing the number of un-occupied final states (reducing the QW Fermi-level), the electron’s interaction with the polariton is increasing dramatically. As a result, most of the electron’s energy can go toward light-emission in a below 10-fs timescale, faster than any other mechanism in the system (stage (i) in Fig. e below). Since the light-emission can occur before the quasi-thermal equilibrium in the conduction band, we found that an ultra-fast and extremely tunable emission can occur in such structures (Fig. f below). This result is yet another proof that spontaneous emission can completely overcome stimulated emission.
Now, because a single electron interacts so strongly with the light, the emitted polariton can get re-absorbed by the same electron. This phenomenon is in fact non-local Rabi-oscillations with a frequency of about 10 fs (stage (ii) Fig. e below) between the electron wave and the propagating polaritons. Moreover, the possibility of reabsorption of the emitted light cause a tunable shift in the electron effective mass and the quantum well’s bandgap of up to 100 meV (Fig. g below) which is 20% of the original bandgap. Therefore, just by stating the graphene sheet on top of a semiconductor, the semiconductor’s bandgap and its electron’s effective mass would alter due to the possibility of interacting with the vacuum fluctuations of the graphene plasmons.
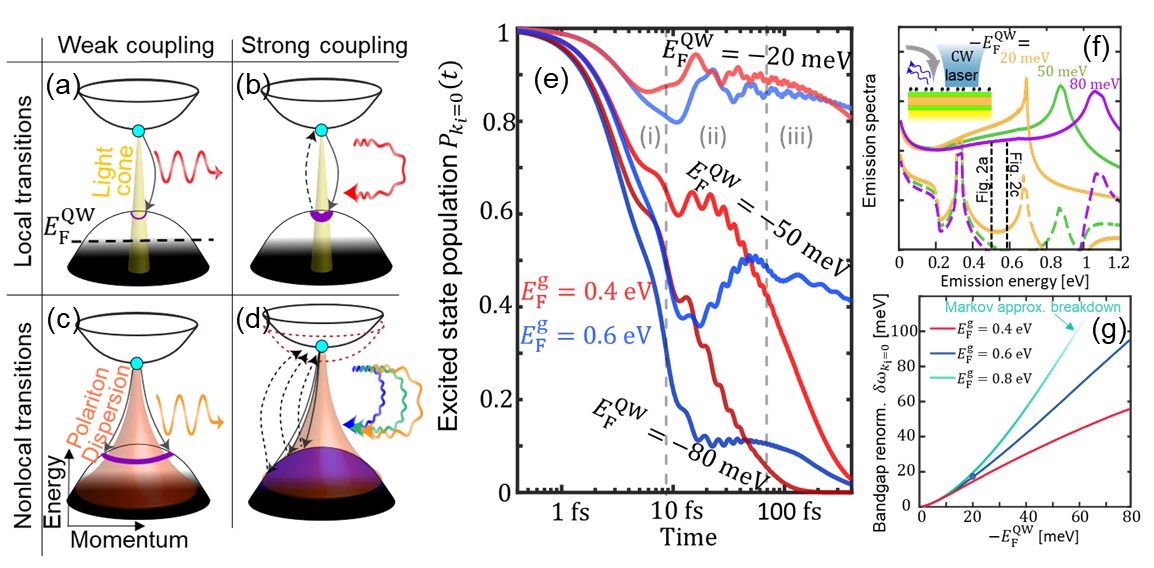
Nonlocal Ultra-Strong Coupling for an ultra-fast light emission and tunable bandgap renormalization. (a-d) The role of nonlocality in reaching ultra-strong coupling (USC) in solids. A general scheme depicting weak coupling (a,c) and strong coupling (b,d) for local (vertical) transitions with photons (light cone in yellow) (a,b) and for nonlocal (non-vertical) transitions with large-momentum polaritons (polariton dispersion in pink) (c,d). (c) The large momenta of the polaritons enable nonlocal transitions and thus open coupling to a wider range of final states (depicted in purple) for the excited electron (turquoise), similar to Fig. c in the first figure.d) Provided strong enough coupling and nonlocal transitions, a single excited electron can couple to all available ground states, even if they are de-tuned from the polaritonic dispersion. This coupling is still limited by the ground state occupation according to the Fermi-Dirac distribution (un\occupied states in black\white). Consequently, these enhanced nonlocal interactions cause an electron-polariton renormalization of the semiconductor bandgap. (e) The time-dependent initial state population probability for different values of Fermi levels of both the graphene and the quantum well (QW). We show the three decay stages. (i) An extremely fast initial decay followed by (ii) Rabi oscillations, and eventually (iii) an exponential decay. (f) The highly tunable expected nearfield emission spectra as a result of a continuous wave (CW) laser excitation. Due to the enhanced optical response, the excited electron would prefer to emit into the nearfield optical excitations, before a quasi-thermal equilibrium is reached in the conduction band. To outcouple the nearfield emission one can consider a metallic tip (solid) or a 20-nm periodic grating (dashed). Inset: Illustration of the suggested experimental scheme. (g) The tunable bandgap renormalization controlled by the graphene and the QW Fermi levels.

