Inverse Cerenkov Radiation
The Cherenkov effect (also called Vavilov-Cherenkov effect) has attracted vast interest since its discovery in 1934 and the Nobel Prize of 1958, yet to this day, all experiments on the subject have been perfectly accounted for by classical electrodynamics. Similarly, all demonstrations of analogous effects in a wide range of fields – such as water waves, acoustics, and even phononics- are also explained entirely classically. This classical Cherenkov effect, and its analogues, enjoy numerous applications16 in particle identification, medical imaging, quantum cascade lasers, nanophotonics, and nonlinear optics. Likewise, experiments using the stimulated Cherenkov effect for electron acceleration and for other electron-laser interactions are also described classically.
Interestingly enough, theoretical studies by Ginzburg and Sokolov that date back to 1940 explored the Cherenkov effect within quantum electrodynamics (QED). However, the effects were considered negligible in practice, and the celebrated Lev Landau even said at the time that “quantum corrections are immaterial” in the Cherenkov effect. Despite this critique, recent papers have built on these studies and predicted new intrinsic quantum phenomena in the Cherenkov effect. These phenomena led to a far more fundamental puzzle with consequences for the foundations of light-matter interactions: Does general radiation emission depend on the wavefunction shape of the radiating particle or can it always be described in terms of a classical point charge?
Light and matter in sync
Strong and efficient coupling of free-electrons and light would let us reach new energy regimes that were not available before and help us observe and study new and interesting phenomena. Also, it would lead to better cost-effective interactions: we could use less laser’s power yet achieving the same results (important for technology).
The two main key points for strong and efficient electron-light interactions are:
- Phase matching
- Length/time of interaction
Phase-matching leads to an efficient interaction. It can be explained intuitively by syncing the free-electron wavefunction’s velocity with the light phase velocity along the propagation direction of the electron. This way, each part of the free-electron wavefunction interacts with a constant electromagnetic field (instead of an oscillations of the EM field) and the interaction strength is accumulated over the interaction length/time. To fully incorporate this efficient coupling we need to keep this condition for as long distance as possible (or for the longest time possible).
In our work from 2020 we designed a special experimental setup to achieve such strong and efficient interaction between a free-electron wavefunction and a travelling light wave through prism coupling.
Efficient coupling
To achieve a phase-matched interaction, we directed the light pulse through a glass prism at a precise angle to reduce its phase velocity such that it will exactly match the free-electron velocity. This type of interaction can be explained by the inverse-Cherenkov effect and the precise angle is the famous Cherenkov radiation emission cone’s angle. More on the quantum Cherenkov effect can be read on an article published on our paper in Nature’s blog (On Your Wavelength).
Strong coupling
Next, we wanted the interaction to last for as long as possible. This was an experimental challenge since we had to keep the free-electron beam parallel to the prism’s surface for as long as possible – known as a grazing angle interaction. We developed a technique for aligning the electron beam and the prism and achieved an interaction length of hundreds of microns (3 orders of magnitude longer than typical interactions in our field of hundreds of nanometers).
More details can be seen in an article published on phys.org and also in Hebrew on Haaretz and Little Big Science.
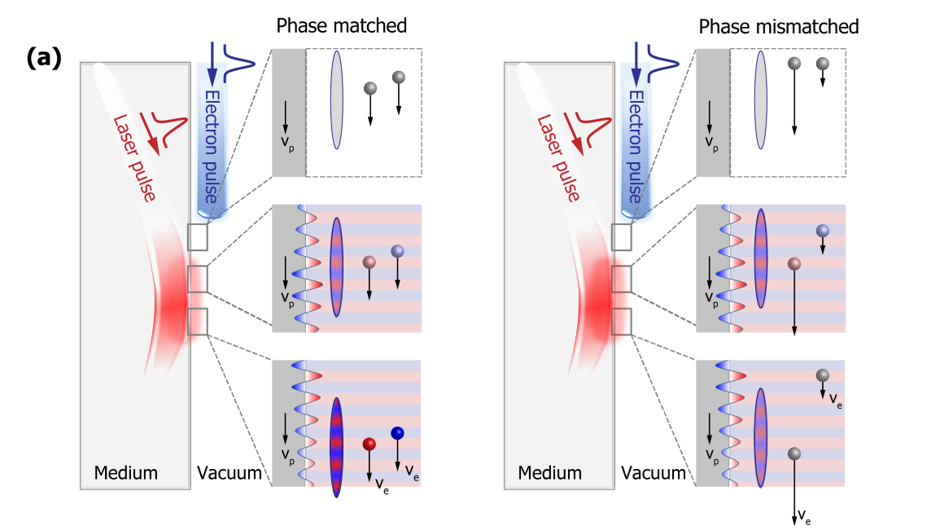
Illustration of the phase-matched/mismatched effect for both the classical and quantum interpretations. The electron interacts with an evanescent field generated by a laser that is totally internally reflected from an interface. Classical: a point electron (small particle) is matched with the light field maximum/minimum and results in accumulated acceleration/deceleration. Quantum: an electron wavefunction is matched with multiple cycles of the light field simultaneously and results in a significant modulation of the wavefunction.

